Cryptography
Cryptography, or cryptology, is the practice and study of techniques for secure communication in the presence of third parties called adversaries.
More generally, cryptography is about constructing and analyzing protocols that prevent third parties or the public from reading private messages; various aspects in information security such as data confidentiality, data integrity, authentication, and non-repudiation are central to modern cryptography.

Modern cryptography exists at the intersection of the disciplines of mathematics, computer science, electrical engineering, communication science, and physics. Applications of cryptography include electronic commerce, chip-based payment cards, digital currencies, computer passwords, and military communications.
Cryptography basics
Cryptography prior to the modern age was effectively synonymous with encryption, the conversion of information from a readable state to apparent nonsense. The originator of an encrypted message shares the decoding technique only with intended recipients to preclude access from adversaries. The cryptography literature often uses the names Alice (“A”) for the sender, Bob (“B”) for the intended recipient, and Eve (“eavesdropper”) for the adversary. Since the development of rotor cipher machines in World War I and the advent of computers in World War II, the methods used to carry out cryptology have become increasingly complex and its application more widespread.
Terminology
The first use of the term cryptograph (as opposed to cryptogram) dates back to the 19th century—originating from The Gold-Bug, a novel by Edgar Allan Poe. Until modern times, cryptography referred almost exclusively to encryption, which is the process of converting ordinary information (called plaintext) into unintelligible form (called ciphertext).
Decryption is the reverse, in other words, moving from the unintelligible ciphertext back to plaintext. A cipher (or cypher) is a pair of algorithms that create the encryption and the reversing decryption. The detailed operation of a cipher is controlled both by the algorithm and in each instance by a “key”. The key is a secret (ideally known only to the communicants), usually a short string of characters, which is needed to decrypt the ciphertext.
Formally, a “cryptosystem” is the ordered list of elements of finite possible plaintexts, finite possible cyphertexts, finite possible keys, and the encryption and decryption algorithms which correspond to each key. Keys are important both formally and in actual practice, as ciphers without variable keys can be trivially broken with only the knowledge of the cipher used and are therefore useless (or even counter-productive) for most purposes.
Cryptanalysis is the term used for the study of methods for obtaining the meaning of encrypted information without access to the key normally required to do so; i.e., it is the study of how to crack encryption algorithms or their implementations. Some use the terms cryptography and cryptology interchangeably in English, while others (including US military practice generally) use cryptography to refer specifically to the use and practice of cryptographic techniques and cryptology to refer to the combined study of cryptography and cryptanalysis. English is more flexible than several other languages in which cryptology (done by cryptologists) is always used in the second sense above. RFC 2828 advises that steganography is sometimes included in cryptology.
Modern cryptography
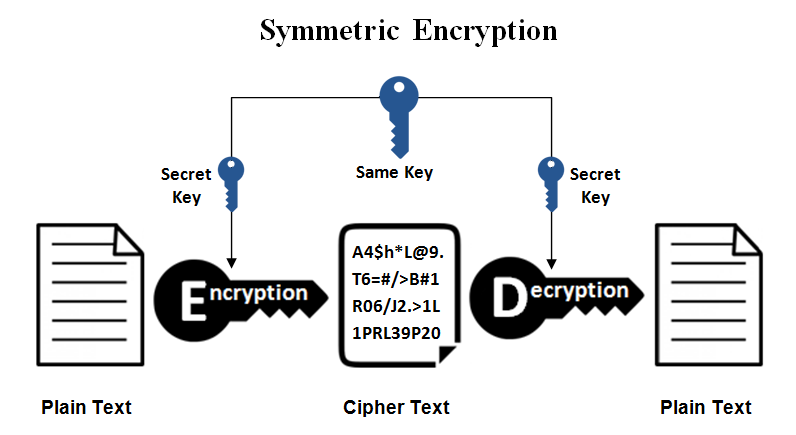
Symmetric-key cryptography refers to encryption methods in which both the sender and receiver share the same key (or, less commonly, in which their keys are different, but related in an easily computable way). This was the only kind of encryption publicly known until June 1976. logic diagram showing International Data Encryption Algorithm cypher process One round (out of 8.5) of the IDEA cipher, used in most versions of PGP and OpenPGP compatible software for time-efficient encryption of messages Symmetric key ciphers are implemented as either block ciphers or stream ciphers.
A block cipher enciphers input in blocks of plaintext as opposed to individual characters, the input form used by a stream cipher. Cryptographic hash functions are a third type of cryptographic algorithm. They take a message of any length as input, and output a short, fixed length hash, which can be used in (for example) a digital signature. For good hash functions, an attacker cannot find two messages that produce the same hash.
Some examples
MD4 is a long-used hash function that is now broken; MD5, a strengthened variant of MD4, is also widely used but broken in practice. The US National Security Agency developed the Secure Hash Algorithm series of MD5-like hash functions: SHA-0 was a flawed algorithm that the agency withdrew; SHA-1 is widely deployed and more secure than MD5, but cryptanalysts have identified attacks against it; the SHA-2 family improves on SHA-1, but is vulnerable to clashes as of 2011; and the US standards authority thought it “prudent” from a security perspective to develop a new standard to “significantly improve the robustness of NIST’s overall hash algorithm toolkit. ”
Thus, a hash function design competition was meant to select a new U.S. national standard, to be called SHA-3, by 2012. The competition ended on October 2, 2012 when the NIST announced that Keccak would be the new SHA-3 hash algorithm. Unlike block and stream ciphers that are invertible, cryptographic hash functions produce a hashed output that cannot be used to retrieve the original input data.
Cryptographic hash functions are used to verify the authenticity of data retrieved from an untrusted source or to add a layer of security.
Public-key cryptography
Symmetric-key cryptosystems use the same key for encryption and decryption of a message, although a message or group of messages can have a different key than others. A significant disadvantage of symmetric ciphers is the key management necessary to use them securely. Each distinct pair of communicating parties must, ideally, share a different key, and perhaps for each ciphertext exchanged as well. The number of keys required increases as the square of the number of network members, which very quickly requires complex key management schemes to keep them all consistent and secret.
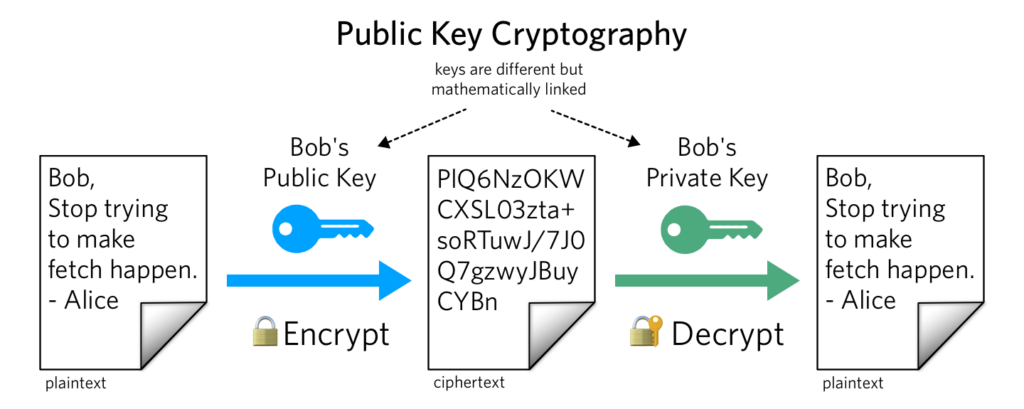
In public-key cryptosystems, the public key may be freely distributed, while its paired private key must remain secret.
In a public-key encryption system, the public key is used for encryption, while the private or secret key is used for decryption.
While Diffie and Hellman could not find such a system, they showed that public-key cryptography was indeed possible by presenting the Diffie–Hellman key exchange protocol, a solution that is now widely used in secure communications to allow two parties to secretly agree on a shared encryption key. The X.509 standard defines the most commonly used format for public key certificates.
Public-key cryptography is also used for implementing digital signature schemes. A digital signature is reminiscent of an ordinary signature; they both have the characteristic of being easy for a user to produce, but difficult for anyone else to forge. Digital signatures can also be permanently tied to the content of the message being signed; they cannot then be ‘moved’ from one document to another, for any attempt will be detectable. In digital signature schemes, there are two algorithms: one for signing, in which a secret key is used to process the message (or a hash of the message, or both), and one for verification, in which the matching public key is used with the message to check the validity of the signature.
RSA and DSA are two of the most popular digital signature schemes. Digital signatures are central to the operation of public key infrastructures and many network security schemes (e.g., SSL/TLS, many VPNs, etc.).
Public-key algorithms are most often based on the computational complexity of “hard” problems, often from number theory. For example, the hardness of RSA is related to the integer factorization problem, while Diffie–Hellman and DSA are related to the discrete logarithm problem.
The security of elliptic curve cryptography is based on number theoretic problems involving elliptic curves. Because of the difficulty of the underlying problems, most public-key algorithms involve operations such as modular multiplication and exponentiation, which are much more computationally expensive than the techniques used in most block ciphers, especially with typical key sizes. As a result, public-key cryptosystems are commonly hybrid cryptosystems, in which a fast high-quality symmetric-key encryption algorithm is used for the message itself, while the relevant symmetric key is sent with the message, but encrypted using a public-key algorithm.
Cryptanalysis
In connection with his WWII work at Bell Labs, Claude Shannon proved that the one-time pad cipher is unbreakable, provided the key material is truly random, never reused, kept secret from all possible attackers, and of equal or greater length than the message. Most ciphers, apart from the one-time pad, can be broken with enough computational effort by brute force attack, but the amount of effort needed may be exponentially dependent on the key size, as compared to the effort needed to make use of the cipher.
In such cases, effective security could be achieved if it is proven that the effort required (i.e., “work factor”, in Shannon’s terms) is beyond the ability of any adversary. This means it must be shown that no efficient method (as opposed to the time-consuming brute force method) can be found to break the cipher. Since no such proof has been found to date, the one-time-pad remains the only theoretically unbreakable cipher.
Cryptosystems
One or more cryptographic primitives are often used to develop a more complex algorithm, called a cryptographic system, or cryptosystem. Cryptosystems (e.g., El-Gamal encryption) are designed to provide particular functionality (e.g., public key encryption) while guaranteeing certain security properties (e.g., chosen-plaintext attack (CPA) security in the random oracle model).
Cryptosystems use the properties of the underlying cryptographic primitives to support the system’s security properties. As the distinction between primitives and cryptosystems is somewhat arbitrary, a sophisticated cryptosystem can be derived from a combination of several more primitive cryptosystems.
In many cases, the cryptosystem’s structure involves back and forth communication among two or more parties in space (e.g., between the sender of a secure message and its receiver) or across time (e.g., cryptographically protected backup data). Such cryptosystems are sometimes called cryptographic protocols.

A good example of cryptosystems are blockchains (Bitcoin, Ethereum, Cardano, Litecoin, Ripple, Tron, Stellar etc.)
